So.. what is machine learning? (#NoCodeIntro)
TL;DR
Strap in, this is a long one. If the title of the post isn't enough of a summary for you but you think that this "TL;DR" is too long then this probably isn't the article for you!
A previous job I had was, in a nutshell, working on improving searching for files and documents by incorporating machine learning algorithms - eg. if I've found a PowerPoint presentation that I produced five years ago on my computer and I want to find the document that I made with loads of notes and research relating to it, how can I find it if I've forgotten the filename or where I stored it? This product could pull in data from many data sources (such as Google Docs, as well as files on my computer) and it could, amongst other things, use clever similarity algorithms to suggest which documents may be related to that presentation. This is just one example but even this is a bit of a mouthful! So when people outside of the industry asked me what I did, it was often hard to answer them in a way that satisfied us both.
This came to a head recently when I tried to explain to someone semi-technical what the difference actually was between machine learning and.. er, not machine learning. The "classic approach", I suppose you might call it. I tried hard but I made a real meal of the explanation and doing lots of hand waving did not make up for a lack of whiteboard, drawing apparatus or a generally clear manner to explain. So, for my own peace of mind (and so that I can share this with them!), I want to try to describe the difference at a high level and then talk about how machine learning can work (in this case, I'll mostly be talking about "supervised classification" - I'll explain what that means shortly and list some of the other types) in a way that is hopefully understandable without requiring any coding or mathematical knowledge.
The short version
- The "classic approach" involves the programmer writing very specific code for every single step in a given process
- "Supervised classification" involves the programmer writing some quite general (ie. not specific to the precise task) code and then giving it lots of information along with a brief summary of each piece of information (also known as a label) so that it can create a "trained model" that can guess how to label new information that it hasn't seen before
What this means in practice
An example of the first ("classic") approach might be to calculate the total for a list of purchases:
- The code will look through each item and lookup in a database what rate of tax should be applied to it (for example, books are exempt from VAT in the UK)
- If there is a tax to apply then the tax for the item will be calculated and this will be added to the initial item's cost
- All of these costs will be added up to produce a total
This sort of code is easy to understand and if there are any problems encountered in the process then it's easy to diagnose them. For example, if an item appeared on the list that wasn't in the database - and so it wasn't possible to determine whether it should be taxed or not - then the problem could easily stop with an "item not found in database" error. There are a lot of advantages to code being simple to comprehend and having it easy to understand how and why bad things have happened.
(Anyone involved in coding knows that dealing with "the happy path" of everything going to plan is only a small part of the job and it's often when things go wrong that life gets hard - and the easier it is to understand precisely what happened when something does go wrong, the better!)
An example of the second ("machine learning") approach might be to determine whether a given photo is of a cat or a dog:
- There will be non-specific (or "generic") code that is written that can take a list of "labelled" items (eg. this is a picture of a cat, this is a picture of a dog) and use it to predict an unseen and unlabelled item (eg. here is a picture - is it a cat or a dog?) - this code is considered to be generic because nothing in the way it is written relates to cats or dogs, all it is intended to do is be able to receive lots of labelled data and produce a trained model that can make predictions on future items
- The code will be given a lot of labelled data (maybe there are 10,000 pictures of cats and 10,000 pictures of dogs) and it will perform some sort of clever mathematics that allows it to build a model trained to differentiate between cats and dogs - generally, the more labelled data that is provided, the better the final trained model will be at making predictions.. but the more data that there is, the longer that it will take to train
- When it is finished "training" (ie. producing this "trained model"), it will then be able to be given a picture of a cat or a dog and say how likely it is that it thinks it is a cat vs a dog
This sounds like quite a silly example but there are many applications of this sort of approach that are really useful - for example, the same non-specific/generic code could be given inputs that are scans of hospital patients where it is suspected that there is a cancerous growth in the image. It would be trained by being given 1,000s of images that doctors have already said "this looks like a malignant growth" or "this looks like nothing to worry about" and the trained model that would be produced from that information would then be able to take images of patient scans that it's never seen before and predict whether it shows something to worry about.
(This sort of thing would almost certainly never replace doctors but it could be used to streamline some medical processes - maybe the trained model is good enough that if it predicts with more than 90% certainty that the scan is clear then a doctor wouldn't need to look at it but if there was even a 10% chance that it could be a dangerous growth then a doctor should look at it with higher priority)
Other examples could be taken from self-driving cars; from the images coming from the cameras on the car, does it look like any of them indicate pedestrians nearby? Does it look like there are speed limit signs that affect how quickly the car may travel?
The results of the trained model need not be binary (only two options), either - ie. "is this a picture of a cat or is it a picture of a dog?". It could be trained to predict a wide range of different animals, if we're continuing on the animal-recognition example. In fact, an application that I'm going to look at in more depth later is using machine learning to recognise hand-written digits (ie. numbers 0 through 9) because, while this is a very common introductory task into the world of machine learning, it's a sufficiently complicated task that it would be difficult to imagine how you might solve it using the "classic" approach to coding.
Back to the definition of the type of machine learning that I want to concentrate on.. the reason it's referred to as "supervised classification" is two-fold:
- The trained model that it produces has the sole task of taking inputs (such as pictures in the examples above, although there are other forms of inputs that I'll mention soon) and predicting a "classification" for them. Generally, it will offer a "confidence score" for each of the classifications that it's aware of - to continue the cat/dog example, if the trained model was given a picture of a cat then it would hopefully give a high prediction score that it was a cat (generally presented as a percentage) and the less confident it was that it was a cat, the more confident it would be that the picture was of a dog.
- The model is trained by the "labelled data" - it can't guess which of the initial pictures are cats and which are dogs if it's just given a load of unlabelled pictures and no other information to work from. The fact that this data is labelled means that someone has had to go through the process of manually applying these labels. This is the "supervised" aspect.
There are machine learning algorithms (where an "algorithm" is just a set of steps and calculations performed to produce some result) that are described as "unsupervised classification" but the most common example of this would be to train a model on a load of inputs and ask it to split them into groups based upon which it thinks seem most similar. It won't be able to give a name to each group because all it has access to is the raw data of each item and no "label" for what each one represents.
This sort of approach is a little similar to how the "find related documents" technology that I described at the top of this post works - the algorithm looks for "features"* that it thinks makes it quite likely that two documents contain the same sort of content and uses this to produce a confidence score that they may be related. I'll talk about other types of machine learning briefly near the end of this post but, in an effort to give this any semblance of focus, I'm going to stick with talking about "supervised classification" for the large part.
* ("Features" has a specific meaning in terms of machine learning algorithms but I won't go into detail on it right now, though I will later - for now, in the case of similar documents, you can imagine "features" as being uncommon words or phrases that are more likely to crop up in documents that are similar in some manner than in documents that are talking about entirely different subject matters)
Supervised classification with neural networks
Right, now we're sounding all fancy and technical! A "neural network" is a model commonly used for supervised classification and I'm going to go through the steps of explaining how it is constructed and how it works. But first I'm going to try to explain what one is.
The concept of a neural net was inspired by the human brain and how it has neurons that connect to each other with varying strengths. The strengths of the connections are developed based upon patterns that we've come to recognise. The human brain is amazing at recognising patterns and that's why two Chicago researchers in 1944 were inspired to wonder if a similar structure could be used for some form of automated pattern recognition. I'm being intentionally vague here because the details aren't too important and the way that connections are made in the human brain is much more complicated than those in the neural networks that I'll be talking about here, so I only really mention it for a little historical context and to explain some of the names of things.
A neural net has a set of "input neurons" and a set of "output neurons", where the input neurons are connected to the output neurons.
Each time that the network is given a single "input" (such as an image of a cat), that input needs to be broken down into values to feed to the input neurons; these input neurons accept numeric values between 0 and 1 (inclusive of those two values) and it may not immediately be apparent how a picture can be somehow represented by a list of 0-to-1 values but I'll get to that later.
There are broadly two types of classifier and this determines how many output neurons there will be - there are "binary classifiers" (is the answer yes or no; eg. "does this look like a malignant growth or not?") and there are "multi-class classifier" (such as a classifier that tries to guess what kind of fruit an image is of; a banana, an apple, a mango, an orange, etc..). A binary classifier will have one output neuron whose output is a confidence score for the yes/no classification (eg. it is 10% certain that it is not an indication of cancer) while a multi-class classifier will have as many output neurons as there are known outputs (so an image of a mango will hopefully produce a high confidence score for the mango output neuron and a lower confidence score for the output neurons relating to the other types of fruit that it is trained to recognise).
Each connection from the input neurons to the output neurons has a "weight" - a number that represents how strong the connection is. When an "input pattern" (which is the name for the list of 0-to-1 input neuron values that a single input, such as a picture of a cat, maybe represented by) is applied to the input neurons, the output neurons are set to a value that is the sum of every input neuron's value that is connected to it multiplied by the weight of the connection.
I know that this is sounding very abstract, so let's visualise some extremely simple possible neural nets.
Examples that are silly to use machine learning for but which are informative for illustrating the principles
The image below depicts a binary classifier (because there is only one output neuron) where there are only two input neurons. The connections between the two inputs neurons to the single output neuron each have a weight of 0.3.
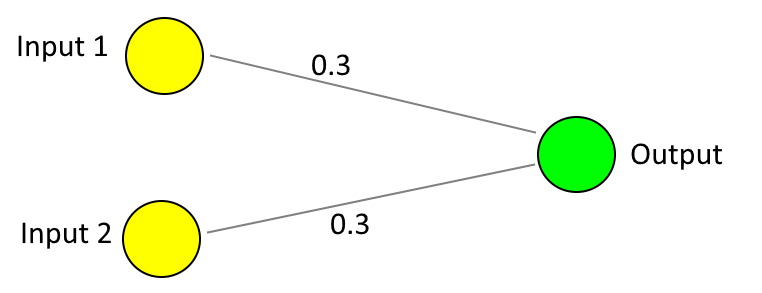
This could be considered to be a trained model for performing a boolean "AND" operation.. if you'll allow me a few liberties that I will take back and address properly shortly.
An "AND" operation could be described as a light bulb that is connected to two switches and the light bulb only illuminates if both of the switches are set to on. If both switches are off then the light bulb is off, if only one of the switches is on (and the other is off) then the light bulb is off, if both switches are on then the light bulb turns on.
Since the neuron inputs have to accept values between 0 and 1 then we could consider an "off" switch as being a 0 input and an "on" switch as being a 1 input.
If both switches are off then the value at the output is (0 x 0.3) + (0 x 0.3) = 0 because we take the input values, multiply them by their connection weights to the output and add these values up.
If one switch is on and the other is off then the output is either (1 x 0.3) + (0 x 0.3) or (0 x 0.3) + (1 x 0.3), both of which equal 0.3 and we'll consider 0.5 to be the cut-off point at which we consider the output to be "on".
If both switches are on then the output is (1 x 0.3) + (1 x 0.3) = 0.6, which is greater than 0.5 and so we consider the output to be on, which is the result that we wanted!
Just in case it's not obvious, this is not a good use case for machine learning - this is an extremely simple process that would be written much more obviously in the "classic approach" to programming.
Not only would it be simpler to use the classic approach, but this is also not suited for machine learning because we know all of the possible input states and what their outputs should be - we know what happens when both switches are off and when precisely one switch is on and when both switches are on. The amazing thing with machine learning is that we can produce a trained model that can then make predictions about data that we've never seen before! Unlike this two-switches situation, we can't possibly examine every single picture of either a cat or a dog in the entire world but we can train a model to learn from one big set of pictures and then perform the crucial task of cat/dog identification in the future for photos that haven't even been taken yet!
For a little longer, though, I'm going to stick with some super-simple boolean operation examples because we can learn some important concepts.
Where the "AND" operation requires both inputs to be "on" for the output to be "on", there is an "OR" operation where the output will be "on" if either or both of the inputs are on. The weights on the network shown above will not work for this.
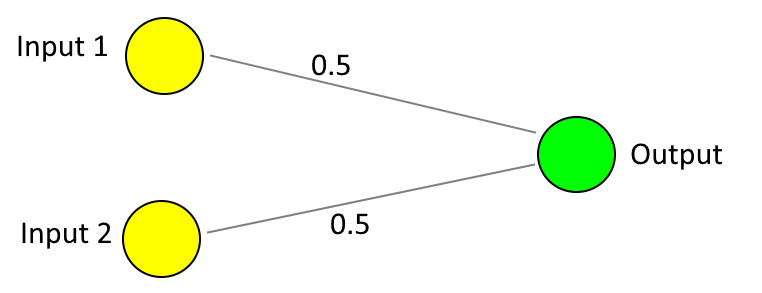
Now this second network would work to imitate an OR operation - if both switches are off then the output is (0 x 0.5) + (0 x 0.5) = 0, if precisely one switch is on then the output is (1 x 0.5) + (0 x 0.5) or (0 x 0.5) + (1 x 0.5) = 0.5, if both switches are on then the output is (1 x 0.5) + (1 x 0.5) = 1. So if both switches are off then the output is 0, which means the light bulb should be off, but if one or both of the switches are on then the output is at least 0.5, which means that the light bulb should be on.
This highlights that the input neurons and output neurons determine the form of the data that the model can receive and what sort of output/prediction it can make - but it is the weight of the connections that control what processing occurs and how the input values contribute in producing produce the output value.
- *(Note that there can be more layers of neurons in between the input and output layer, which we'll see an example of shortly)
In both of the two examples above, it was as if we were looking at already-trained models for the AND and the OR operations but how did they get in that state? Obviously, for the purposes of this post, I made up the values to make the examples work - but that's not going to work in the real world with more complex problems where I can't just pull the numbers out of my head; what we want is for the computer to determine these connection weight values and it does this by a process of trial and improvement and it is this act that is the actual "machine learning"!
The way that it often works is that, as someone who wants to train a model, I decide on the number of inputs and outputs that are appropriate to my task and then the computer has a representation of a neural network of that shape in its memory where it initially sets all of the connection weights to random values. I then give it my labelled data (which, again, is a list of inputs and the expected output - where each individual "input" is really a list of input values that are all 0-1) and it tries running each of those inputs through its neural network and compares the calculated outputs to the outputs that I've told it to expect. Since this first attempt will be using random connection weights, the chances are that a lot of its calculated output will not match the outputs that I've told it to expect. It will then try to adjust the connection weights so that hopefully things get a bit closer and then it will try running all of the inputs through the neural network with the new weights and see if the calculated outputs are closer to the expected output. It will do this over and over again, making small adjustments to the connection weights each time until it produces a network with connection weights that calculate the expected output for every input that I gave it to learn with.
The reason that the weights that it uses initially are random values (generally between 0 and 1) is that the connection weight values can actually be any number that makes the network operate properly. While the input values are all 0-1 and the output value should end up being 0-1, the connection weights could be larger than one or they could be negative; they could be anything! So your first instinct might be "why set them all to random values instead of setting them all to 0.5 initially" and the answer is that while 0.5 is the mid-point in the allowable ranges for the input values and the output values, there is no set mid-point for the connection weight values. You may then wonder why not set them all to zero because that sounds like it's in the middle of "all possible numbers" (since the weights could be positive or they could be negative) and the machine learning could then either change them from zero to positive or negative as seems appropriate.. well, at the risk of skimming over details, numbers often behave a little strangely in some kinds of maths when zeroes are involved and so you generally get better results starting with random connection weight values, rather than starting with them all at zero.
Let's imagine, then, that we decided that we wanted to train a neural network to perform the "OR" operation. We know that there are two inputs required and one output. And we then let the computer represent this model in memory and have it give the connections random weight values. Let's say that it picks weights 0.9 and 0.1 for the connections from Input1-to-Output and Input2-to-Output, respectively.
We know that the labelled data that we're training with looks like this:
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
.. and the first time that we tried running these inputs through our 0.9 / 0.1 connection weight neural network, we'd get these results:
| Input 1 | Input 2 | Calculated Output | Expected Output | Is Correct |
|---|---|---|---|---|
| 0 | 0 | (0x0.9) + (0x0.1) = 0.0 | 0 | Yes (0.0 < 0.5 so consider this 0) |
| 0 | 1 | (0x0.9) + (1x0.1) = 0.1 | 1 | No (0.1 < 0.5 so consider this 0 but we wanted 1) |
| 1 | 0 | (1x0.9) + (0x0.1) = 0.9 | 1 | Yes (0.9 >= 0.5 so consider this 1) |
| 1 | 1 | (1x0.9) + (1x0.1) = 1.0 | 1 | Yes (1.9 >= 0.5 so consider this 1) |
Unsurprisingly (since completely random connection weights were selected), the results are not correct and so some work is required to adjust the weight values to try to improve things.
I'm going to grossly simplify what really happens at this point but it should be close enough to illustrate the point. The process tries to improve the model by repeatedly running every input pattern through the model (the input patterns in this case are (0, 0), (0, 1), (1, 0), (1, 1)) and comparing the output of the model to the output that is expected for each input pattern (as we know (0, 0) should have an output of < 0.5, while any of the input patterns (0, 1), (1, 0) and (1, 1) should have an output of >= 0.5). When there is a discrepancy in the model's output and the expected output, it will adjust one or more of the connection weights up and down.. then it will do it again and hopefully find that the calculated outputs are closer to the expected outputs, then again and again until the model's calculated outputs for every input pattern match the expected outputs.
So it will first try the pattern (0, 0) and the output will be 0 and so no change is needed there.
Then it will try (0, 1) and find that the output is too low and so it will increase the weight of the connections slightly, so now maybe they go from 0.9 / 0.1 to 0.91 / 0.11.
Then it will try (1, 0) with the new 0.91 / 0.11 weights and find that it gets the correct output (more than 0.5) and so make no change.
Then it will try (1, 1) with the same increased 0.91 / 0.11 weights and find that it still gets the correct output there and so make no more changes.
After this adjustment, the input pattern (0, 1) will still be too low (0 x 0.9) + (1 x 0.11) and so it will have to go round again.
It might continue doing this multiple times until the weights end up something like 0.5 / 1.4 and now it will have a model that gets all of the right values!
| Input 1 | Input 2 | Calculated Output | Expected Output | Is Correct |
|---|---|---|---|---|
| 0 | 0 | (0x1.4) + (0x0.5) = 0.0 | 0 | Yes (0.0 < 0.5 so consider this 0) |
| 0 | 1 | (0x1.4) + (1x0.5) = 0.5 | 1 | Yes (0.5 >= 0.5 so consider this 1) |
| 1 | 0 | (1x1.4) + (0x0.5) = 1.4 | 1 | Yes (1.4 >= 0.5 so consider this 1) |
| 1 | 1 | (1x1.4) + (1x0.5) = 1.9 | 1 | Yes (1.9 >= 0.5 so consider this 1) |
That's the very high-level gist, that it goes round and round in trying each input pattern and comparing the computed output to the expected output until the computed and expected outputs match. Great success!
(I'm not going to go into any more detail about how this weight-adjusting process works because I'm trying to avoid digging into any code in this post - just be aware that this process of calculating the output for each known input and then adjusting the connection weights and retrying until the output values are what we expect for each set of inputs is the actual training of the model, which I'll be referring to multiple times throughout the explanations here)
Now, there are a few things that may seem wrong based upon what I've said previously and how exactly it adjusts those weights through trial-and-improvement:
- The calculations here show that the four outputs are 0.0, 0.5, 1.4 and 1.9 but I said earlier that the input values should all be in the range 0-1 and the output values should be in the same range of 0-1
- Why does it adjust the weights so slowly when it needs to alter them; why would it only add 0.01 to the weight that connects Input1-to-Output each time?
Because I'm contrary, I'll address the second point first. If the weights were increased too quickly then the outputs may then "overshoot" the target output values that we're looking for and the next time that it tries to improve the values, it may find that it has to reduce them. Now, in this simple case where we're trying to model an "OR" operation, that's not going to be a problem because the input pattern (0, 0) will always get an output of 0 since it is calculated as (0 x Input1-to-Output-connection-weight) + (0 x Input2-to-Output-connection-weight) and that will always be 0, while the other three input patterns should all end up with an output of 0.5 or greater. However, for more complicated models, there will be times when weights need to be reduced in some cases as well as increased. If the changes made to the weights are too large then they might bounce back and forth on each attempt and ever settle into the correct values, so smaller adjustments are more likely to result in training a model that matches the requirements but at the cost of having to go round and round on the trial-and-improvement attempts more often.
This means that it will take longer to come to the final result and this is one of the issues with machine learning - for more complicated models, there can be a huge number of these trial-and-improvement attempts and each attempt has to run every input pattern through the model. When I was talking about training a model with 10,000 pictures of cats and 10,000 pictures of dogs and all these inputs have to be fed through a neural network until the outputs are correct then it can take a long time. That's not the case here (where there are only 4 input patterns and it's a very simple network) but for larger cases, there can be a point where you allow the model to train for a certain period and then accept that it won't be perfect but hope that it's good enough for your purposes, as a compromise against how long it takes to train - it can take days to train some really complex models with lots and lots of labelled data! Likewise, another challenge/compromise is trying to decide how quickly the weights should be adjusted - the larger the changes that it makes to the weight values of connections between neurons, the closer that it can get to a good result but it might actually make it impossible to get the best possible result if it keeps bouncing some of the weights back and forth, as I just explained!
Now to address the first point. There's a modicum of maths involved here but you don't have to understand it in any great depth. I've been pretending that the way to calculate the output value on our network is to take (Input1's value x the Input1-to-Output's connection weight) + (Input2's value x the Input2-to-Output's connection weight) but, as we've just seen, this result of this can be greater than 1 and input values and output values are all supposed to be within the 0-1 range. In fact, using this calculation, it would be possible to get a negative output value because neuron connection weights can be negative (I'll explain why in some more examples of machine learning a little later on) and that would also mean that the output value would fall outside of the 0-1 range that we require.
To fix this, we take the simple calculation that I've been using so far and pass the value through a formula that can take any number and squash it into the 0-1 range. While there are different formula options for neural networks, a common one is the "sigmoid function" and it would look like this if it was drawn on a graph (picture courtesy of Wikipedia) -
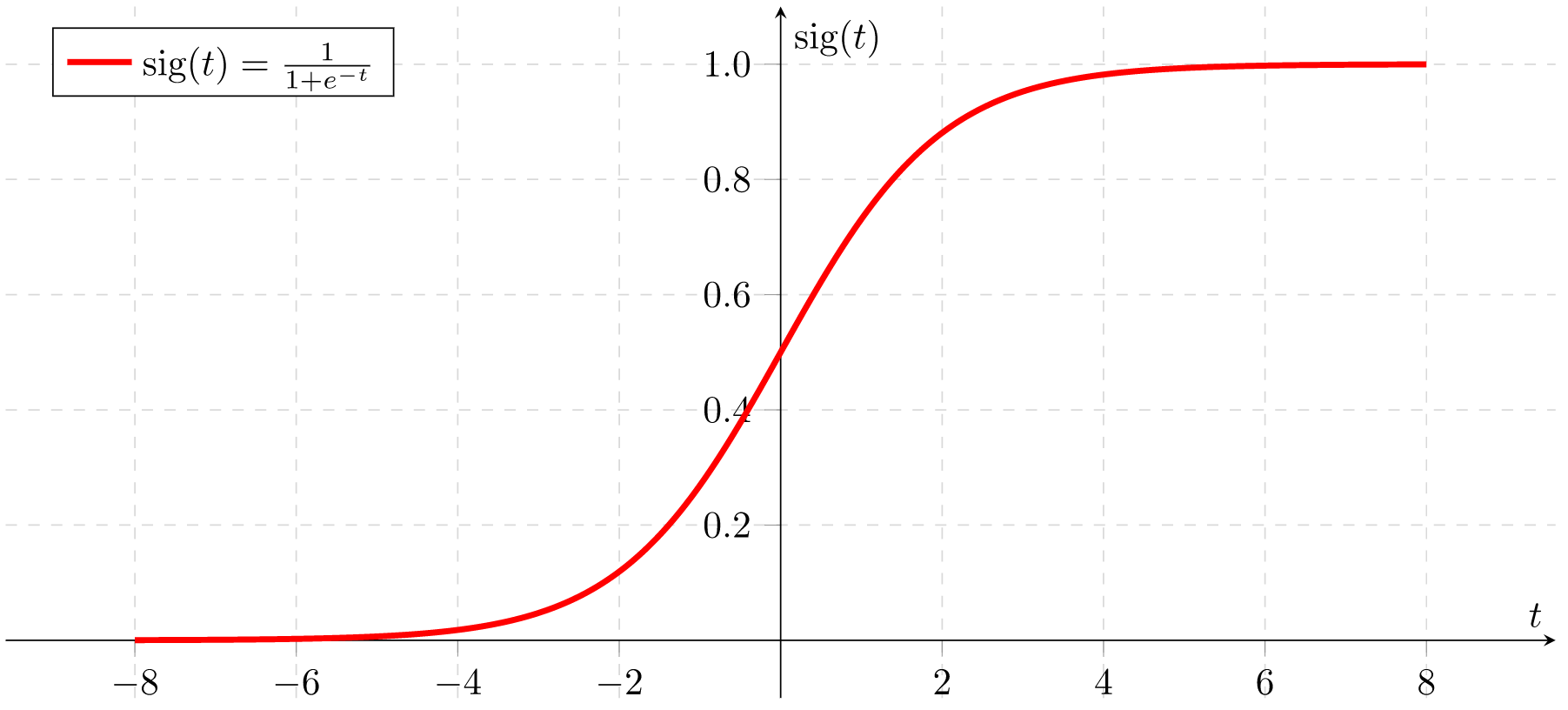
Although this graph only shows values from -8 to +8, you can see that its "S shape" means that the lines get very flat the larger that the number is. So if the formula is given a value of 0 then the result will be 0.5, if it's given a value of 2 then the result will be about 0.88, if it's given a value of 4 then the result is about 0.98, it's given a value of 8 then it's over 0.999 and the larger the value that the function is given the closer that the result will be to 1. It has the same effect for negative numbers - negative numbers that are -8 or larger (-12, -100, -1000) will all return a value very close to 0.
The actual formula for this graph is shown on the top left of the image ("sig(t) = 1 / (1 + e^-t)") but that's really not important to us right now, what is important is the shape of the graph and how it constrains all possible values to the range 0-1.
If we took the network that we talked about above (that trains a model to perform an "OR" operation and where we ended up with connection weights of 1.4 and 0.5) and then applied the sigmoid function to the calculated output values then we'd find that those weights wouldn't actually work and the machine learning process would have to produce slightly different weights to get the correct results. But I'm not going to worry about that now since the point of that example was simply to offer a very approximate overview of how the trial-and-improvement process works. Besides, we've got a more pressing issue to talk about..
The limits of such a simple network and the concept of "linearly separable" data
The two examples of models that we've trained so far are extremely simple in one important way - if you drew a graph with the four input values on them and were asked to draw a straight line that separated the inputs that should relate to an "off" state from the inputs that should relate to an "on" state then you do it very easily, like this:
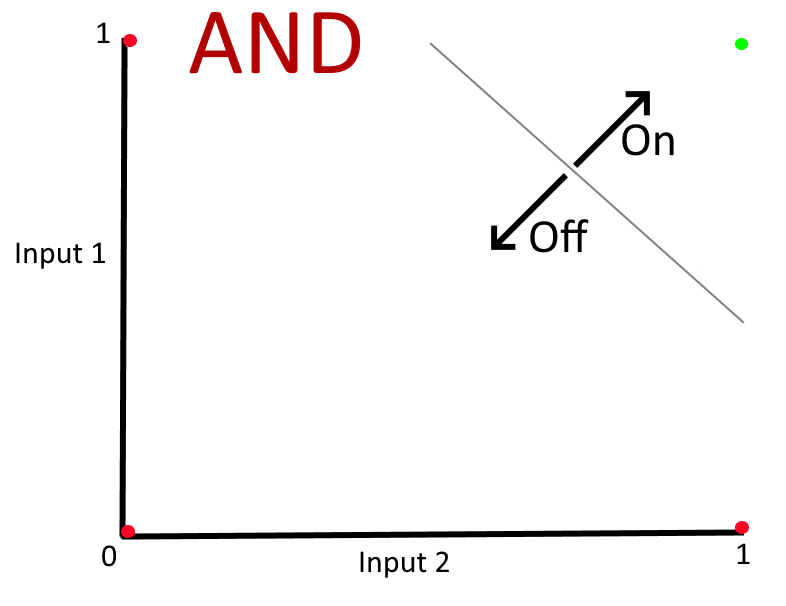
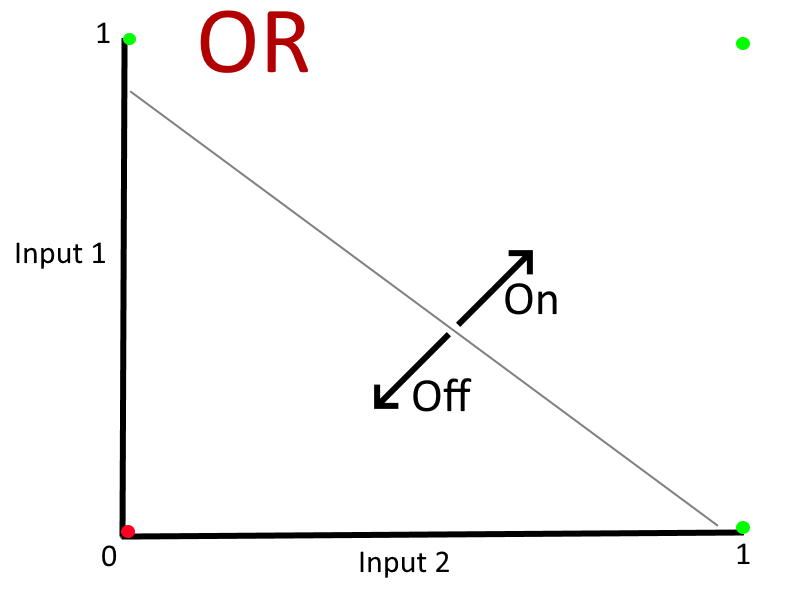
But not all sets of data can be segregated so simply and, unfortunately, it is a limitation to the very simple network shape that we've seen so far (where the input layer is directly connected to the output layer) that it can only work if the data can be split with all positive results on one side of a straight line and all negative results on the other side. Cases where this is possible (such as the "AND" and "OR" examples) are referred to as being "linearly separable" (quite literally, the results in either category can be separated by a single straight line and the model training is, in effect, to work out where that line should lie). Interestingly, there are actually quite a lot of types of data analysis that have binary outcomes that are linearly separable - but I don't want to go too far into talking about that and listing examples because I can't cover everything about machine learning and automated data analysis in this post!
A really simple example of data that is not linearly separable is an "XOR" operation. While I imagine that the "AND" and "OR" operations are named so simply that you could intuit their definitions without a grounding in boolean logic, this may require slightly more explanation. "XOR" is an abbreviation of "eXclusive OR" and, to return to our light bulb and two switches example, the light should be off if both switches are off, it should be on if one of the switches is on but it should be off if both of the switches are on. On the surface, this sounds like a bizarre situation but it's actually encountered in nearly every two-storey residence in the modern world - when you have a light on your upstairs landing, there will be a switch for it downstairs and one upstairs. When both switches are off, the light is off. If you are downstairs and switch the downstairs switch on then the light comes on. If you then go upstairs and turn on your bedroom light, you may then switch the upstairs landing light and the light will go off. At this point, both switches are on but the light is off. So the upstairs light is only illuminated if only one of the switches is on - when they're both on, the light goes off.
If we illustrated this with a graph like the "AND" and "OR" graphs above then you can see that there is no way to draw a single straight line on that graph where every state on one side of the line represents the light being on while every state on the other side of the line represents the light being off.
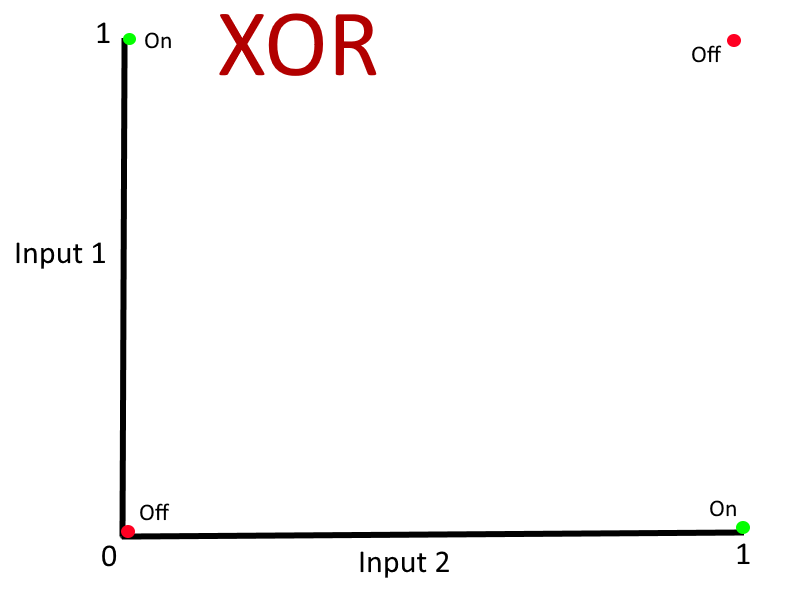
This is a case where the data points (where "data" means "all of the input patterns and their corresponding output values") are not linearly separable. And this means that the simple neural network arrangement that we've seen so far can not produce a trained model that can represent the data. If we tried to train a model in the same way as for AND and OR, the neuron connection weights would go back and forth as the training process kept finding that its "trial-and-improvement" approach continuously came up with at least one wrong result.
There is a solution to this, and that is to introduce another layer of neurons into the graph. In our simple network, there are two "layers" of neurons - the "input" neurons on the left and the "output" neuron on the right. What we would need to do here is add a layer in between, which is referred to as a "hidden layer". A neural network to do this would look something like the following:
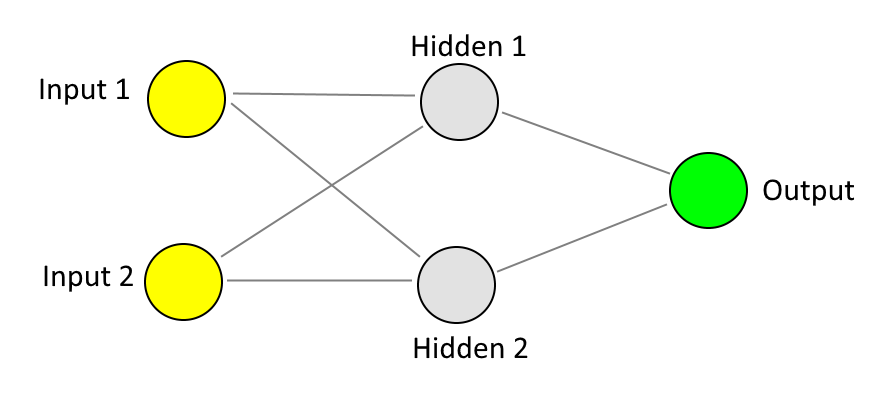
To calculate the output value for any pair of input values, more calculations are required now that we have a hidden layer. Whereas before, we only had to multiple Input 1 by the weight that joined it to the Output and add that value to Input 2 multiplied by its connection we weight, now we have three hidden layer neurons and we have to:
- Multiply Input 1's value by the weight of its connection to Hidden Input 1 and then add that to Input 2's value multiplied by its connection weight to Hidden Input 1 to find Hidden Input 1's "initial value"
- Do the same for Input 1 and Input 2 as they connect to Hidden Input 2
- Apply the sigmoid function for each of the Hidden Input values to ensure that they are between 0 and 1
- Take Hidden Input 1's value multiplied by its connection weight to the output and add that to Hidden Input 2's value multiplied by its connection weight to the Output to find the Output's "initial value"
- Apply the sigmoid function to the Output value
The principle is just the same as when there were only two layers (the Input and Output), except now there are three and we have to take the Input layer and calculate values for the second layer (the Hidden layer) and then use the values there to calculate the value for third and final layer (the Output layer).
(Note that with this extra layer in the model, it is necessary to apply the sigmoid function after each calculation - we could get away with pretending that it didn't exist on the earlier examples but things would fall apart here if kept trying to ignore it)
The learning process described earlier can be applied here to determine what connection weights to use; start with all connection weights set to random values, calculate the final output for every set of inputs, then adjust the connection weights to try to get closer and repeat until the desired results are achieved.
For example, the learning process may result in the following weights being determined as appropriate:
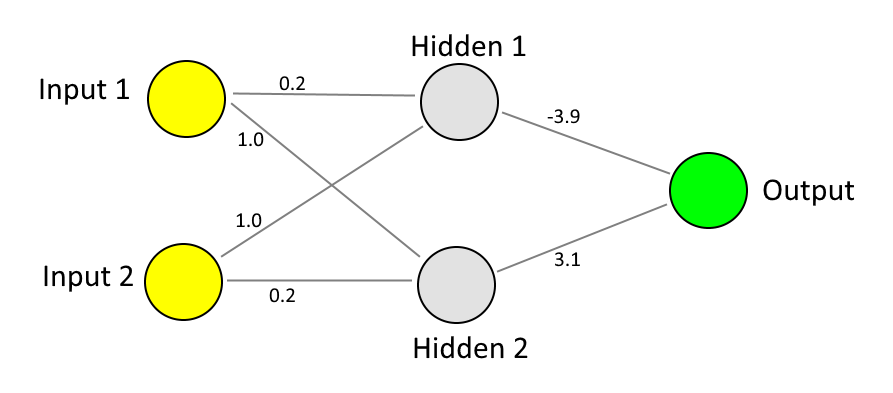
.. which would result in the following calculations occurring for the four sets of inputs (0, 0), (1, 0), (0, 1) and (1, 1) -
| Input 1 | Input 2 | Hidden 1 Initial | Hidden 2 Initial | Hidden 1 Sigmoid | Hidden 2 Sigmoid | Output Initial | Output Sigmoid |
|---|---|---|---|---|---|---|---|
| 0 | 0 | (0x0.2) + (0x0.2) = 0.0 |
(0x1) + (0x1) = 0.0 |
0.50 | 0.50 | (-3.9x0.50) + (3.1x0.50) = -0.40 |
0.17 |
| 0 | 1 | (0x0.2) + (1x0.2) = 0.2 |
(0x1) + (0x1) = 1.0 |
0.69 | 0.98 | (-3.9x0.69) + (3.1x0.98) = 0.35 |
0.80 |
| 1 | 0 | (1x0.2) + (0x0.2) = 0.2 |
(0x1) + (0x1) = 1.0 |
0.69 | 0.98 | (-3.9x0.69) + (3.1x0.98) = 0.35 |
0.80 |
| 1 | 1 | (1x0.2) + (1x0.2) = 0.4 |
(0x1) + (0x1) = 2.0 |
0.83 | 1.00 | (-3.9x0.83) + (3.1x1.00) = -0.14 |
0.36 |
Since we're considering an output greater than or equal to 0.5 to be equivalent to 1 and an output less than 0.5 to be equivalent to 0, we can see that these weights have given us the outputs that we want:
| Input 1 | Input 2 | Calculated Output | Expected Output | Is Correct |
|---|---|---|---|---|
| 0 | 0 | 0.17 | 0 | Yes (0.17 < 0.5 so consider this 0) |
| 0 | 1 | 0.80 | 1 | Yes (0.80 >= 0.5 so consider this 1) |
| 1 | 0 | 0.80 | 1 | Yes (1.80 >= 0.5 so consider this 1) |
| 1 | 1 | 0.36 | 0 | Yes (0.36 < 0.5 so consider this 0) |
How do you know if your data is linearly separable?
Or, to put the question another way, how many layers should your model have??
A somewhat flippant response would be that if you try to specify a model that doesn't have a hidden input layer and the training never stops calculating because it can find weights that perfectly match the data then it's not linearly separable. While it was easy to see with the AND and OR examples above that a training approach of fiddling with the connection weights between the two input nodes and the output should result in values for the model that calculate the outputs correctly, if we tried to train a model of the same shape (two inputs, one output, no hidden layers) for the XOR case then it would be impossible for the computer to find a combination of weights that would correctly calculate outputs for all of the possible inputs. You could claim that because the training process for the XOR case could never finish that it must not be linearly separable - and this is, sort of, technically, correct. But it's not very useful.
One reason that it's not very useful is that the AND, OR, XOR examples only exist to illustrate how neural networks can be arranged, how they can be trained and how outputs are calculated from the inputs. In the real world, it would be crazy to use a neural network for a tiny amount of fixed data for which all of the outputs are known - where a neural network becomes useful is when you use past data to predict future results. An example that I've used before is a fictitious history of a manager's decisions for feature requests that a team receives:
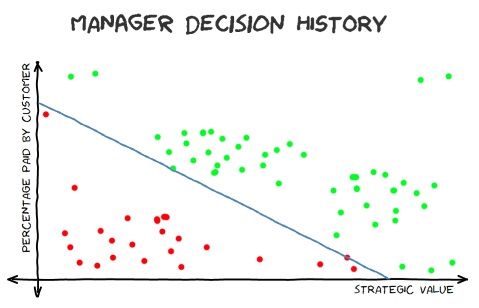
The premise is that every time this manager decides whether to give the green light or not to a feature that has been requested, they consider what strategic importance it has to the company and how much of the work the customer that is requesting it is willing to pay. If it's of high strategic importance and the customer expects to receive such value from it that they are willing to pay 100% of the costs of implementation then surely this manager will be delighted to schedule it! If the customer's budget is less than what it will cost to implement but the feature has sufficiently high strategic value to the company (maybe it will be a feature that could then be sold to many other customers to almost zero cost to the company or maybe it is an opportunity to address an enormous chunk of technical debt) then it still may get the go-ahead! But if the strategic value is low and the customer doesn't have the budget to cover the entire cost of development then the chances are that it will be rejected.
This graph only shows a relatively small number of points and it is linearly separable. As such, the data points on the graph could be used to train a simple two-input (strategic value on a scale of 0-1 and percentage payable by the customer on a scale of 0-1) and single-output binary classifier (the output is whether the feature gets agreed or rejected) neural network. The hope would be that the data used to train it is indicative of how that manager reacts to incoming requests and so it should be possible to take future requests and predict whether that manager is likely to take them on.
However, neural networks are often intended to be used with huge data sets and whenever there is a large amount of data then there is almost always bound to be some outliers present - results that just seem a little out of keeping with those around them. If you were going to train a model like this with 100,000 previous decisions then you might be satisfied with a model that can correctly is 99.9% accurate, which would mean that out of every 100,00 decisions that it might get 100 of them wrong. If you were trying to train a neural network model using 100,000 sets of historical inputs and outputs then you might decide that the computer can stop its training process when the neuron connection weights that it calculates results in outputs being calculated that are correct in 99.9% of cases, rather than hoping that a success rate of 100% can be achieved. This will have the advantage of finishing slightly more quickly but there's always a chance that a couple of those historical input/output entries were written down wrong and, with them included, the data isn't linearly separable - but with them excluded, the data is linearly separable. And so there is a distinction that can be made between whether the entirety of the data is, strictly speaking, linearly separable and whether a simple model can be trained (without any hidden layers) that is a close enough approximation.
The next problem with that simple approach ("if you can't use your data to train a model without hidden layers then it's not linearly separable") is that it suggests that adding in hidden layers will automatically mean that a neural network can be trained with the provided data - which is definitely not correct. Say, for example, that someone believed that this manager would accept or reject feature requests based upon what day of the week it was and what colour tie they were wearing that day. This person could provide historical data for sets of inputs and output - they know that decisions are only made Monday-to-Friday, which so that works itself easily into a 0-1 scale for one input (0 = Monday, 0.2 = Tuesday, etc..) and they have noticed that there are only three colours of tie worn (so a similar numeric value can be associated with each colour). The issue is that there is no correlation between these two inputs and the output, so it's extremely unlikely that a computer would be able to train a simple two-input / one-output model but that does not mean that adding in hidden layers would fix the problem!
This conveniently brings us to the subject of "feature selection". As I touched on earlier, features are measurable aspects of whatever we are trying to make predictions for. The "strategic importance" and "percentage that the customer will pay" were features on the example data before. Feature selection is an important part of machine learning - if you don't capture the right information then it's unlikely that you'll be able to produce something that makes good predictions. When I said before that there could be results in the managerial decision history that don't fit a linearly separable model for these two features, maybe it's not because some of the data points were written down wrong; maybe it's because other factors were at play. Maybe this manager is taking into account other factors such as an agreement with a customer that they can't foot the bill for the entirety of the current feature but they will contribute significantly to another feature that is of high strategic importance to the company but only if this first feature is also completed.
Capturing another feature in the model (perhaps something that reflects how likely the current feature request is to bring in future valuable revenue) is a case of adding another input neuron. So far, we've only seen networks that have two inputs but that has only been the case because they're very easy to talk about and to illustrate as diagrams and to describe calculations for and to draw graphs for! If a third feature was added then all of the calculation processes are essentially the same (if there are three inputs and one output then the output value is calculated by adding together each of the three input values multiplied by their connection weights) and it would still be possible to visualise, it's just that it would be in 3D rather than being a 2D graph. Adding a fourth dimension would mean that it couldn't be easily visualised but the maths and the training process would be the same - and this holds for adding a fifth, sixth or hundredth dimension!
(Other examples of features for the manager decision data might include "team capacity" and "opportunity cost" - would we be sacrificing other, more valuable work if we agree to do this task - and "required timescale for the feature" - is the customer only able to pay for it if it's delivered in a certain time frame, after which they would not be willing to contribute? I'm sure that you wouldn't have to think very hard to conjure up features like this that could explain the results that appear to be "outliers" when only the original two proposed features were considered)
It may well be that adding further relevant features is what makes a data set linearly separable, whereas before - in absence of sufficient information - it wasn't. And, while it can be possible to train a neural network using hidden layers such that it can take all of your historical input/output data and calculate neuron connection weights that make the network appear to operate correctly, it may not actually be useful for making future predictions - where it takes inputs that it hasn't seen before and determines an output. If it can't do this, then it's not actually very useful! A model that is trained to match its historical data but that is poor at making future predictions is said to have been a victim of "overfitting". A way to avoid that is to split up the historical data into "training data" and "test data" as I'll explain in the next section*.
* (I'll also finish answering the question about how many layers you should use and how large they should be!)
A final note on feature selection: In general, gathering more features in your data is going to be better than having fewer. The weights between neurons in a network represent how important the input is that the weight is associated with - this means that inputs/features that make a larger difference to the final output are going to end up with a higher weight in the trained model than inputs/features that are of lower importance. As such, irrelevant features tend to get ignored and so there is little downside to the final trained model from including them - in fact, there will be many circumstances where you don't know beforehand which features are going to be the really important ones and so you may be preventing yourself from training a good model if you exclude data! The downside is that the more inputs that there are, the more calculations need to be performed for each iteration of the "see how good the network is with the current weights and then adjust them accordingly", which can add up quickly if the amount of historical data being used to train is large. But you may well be happier with a model that took a long time to train into a useful state than you would be with a model that was quick to train but which is terrible at making predictions!
A classic example: Reading handwritten numeric digits
An extremely well-known data set that is often used in introductions to machine learning is MNIST; the Modified National Institute of Standards and Technology database, which consists of a large number of 28x28 pixel images of handwritten digits and the number that each image is a picture of (making it a collection of "labelled data" as each entry contains input data, in the form of the image, and an output value, which is the number that the image is known to be of).
It may seem counterintuitive but those 28x28 pixels can be turned into a flat list of 784 numbers (28 x 28 = 784) and they may be used as inputs for a neural network. The main reason that I think that it may be counterintuitive is that by going from a square of pixels to a one-dimensional list of numbers, you might think that valuable information is being discarded in terms of the structure of the image; surely it's important which pixels are above which other pixels or which pixels are to the left of which other pixels? Well, it turns out that discarding this "spatial information" doesn't have a large impact on the results!
Each 28x28 pixel image is in greyscale and every pixel has a brightness value in the range 0-255, which can easily be scaled down to the range 0-1 by dividing each value by 255.
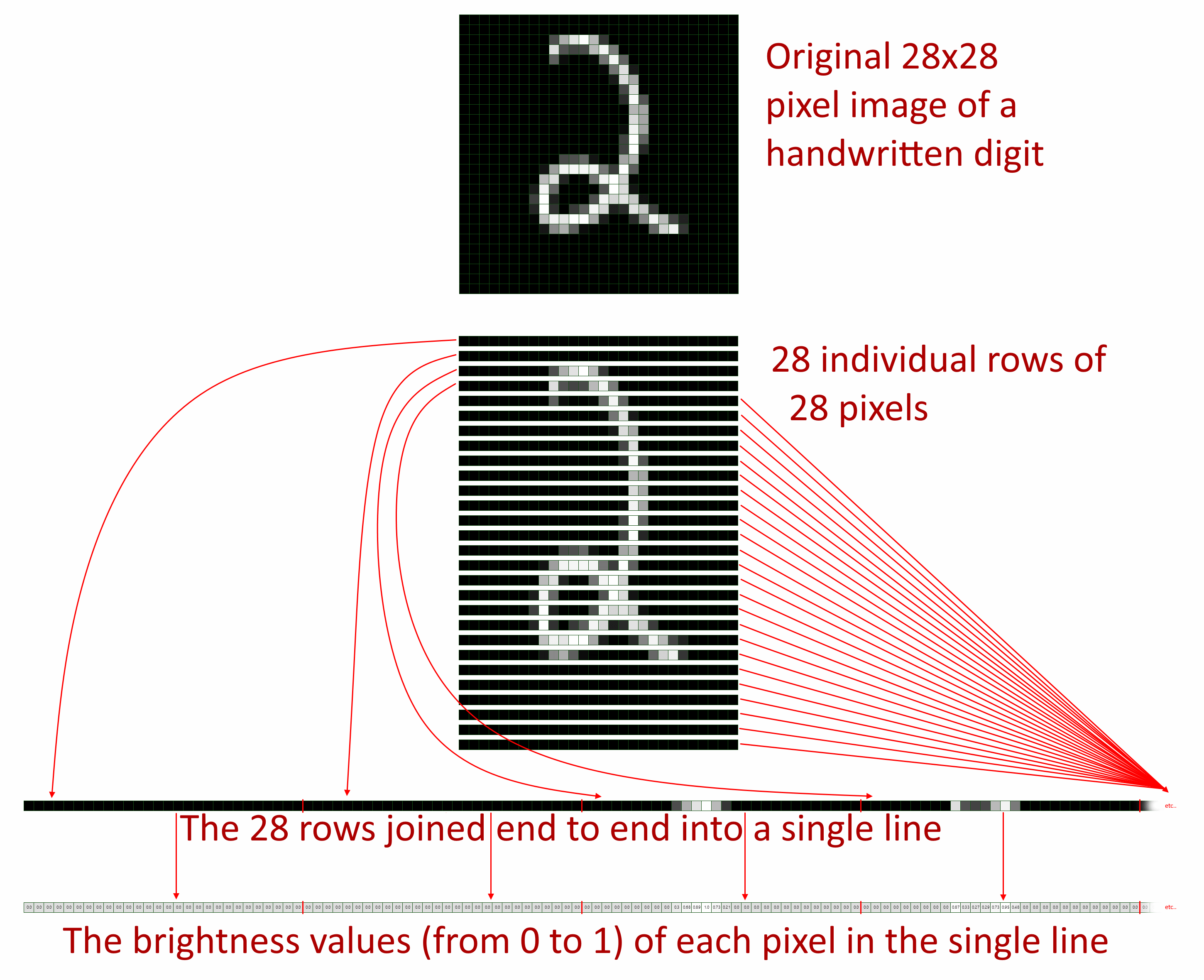
For the outputs, this is not a binary classifier (which is what we've looked at mostly so far); this is a multi-class classifier that has ten outputs because, for any given input image, it should predict whether the digit is 0, 1, etc.. up to 9.
The MNIST data (which is readily available for downloading from the internet) has two sets of data - the training data and the test data. Both sets of data are in the exact same format but the training data contains 60,000 labelled images while the test data contains 10,000 labelled images. The idea behind this split is that we can use the training data to train a model that can correctly give the correct output for each of its labelled images and then we confirm that the model is good by running the test data through it. The test data is the equivalent of "future data" that trained neural networks are supposed to be able to make good predictions for - again, if a neural net is great at giving the right answer for data that it has already seen (ie. the data that it was trained with) but it's rubbish at making predictions for data that it hasn't seen before then it's not a very useful model! Having labelled training data and test data should help us ensure that we don't construct a model that suffers from "overfitting".
Whereas we have so far mostly been looking at binary classifiers that have a single output (where a value of greater than or equal to 0.5 indicates a "yes" and a value less than 0.5 indicates a "no"), here we want a model with ten output nodes - for each of the possible digits. And the 0-1 value that each output will receive will be a "confidence" value for that output. For example, if our trained network processes and image and the outputs for 0, 1, .. 7 are low (say, 0.1) the outputs for 8 and 9 are both similarly high then it indicates that the model is fairly sure that the image is either an 8 or a 9 but it is not very sure which. On the other hand, if 0..7 are low (0.1-ish) and 8 is high (say, 0.9) and 9 is in between (0.6 or so) then the model still thinks that 8 or 9 are the most likely results but, in this case, it is much more confident that 8 is the correct output.
What we know about the model at this point, for sure, is that there are 784 input neurons (for each pixel in the source data) and 10 output neurons (for each possible label for each image). What we don't know is whether we need a hidden layer or not. What we do know in this case, though, is how we can measure the effectiveness of any model that we train - because we train it using the training data and then see how well that trained model predicts the results of the test data. If our trained model gets 99% of the correct answers when we try running the test data through it then we know that we've done a great job and if we only get 10% of the correct answers for our test data then we've not got a good model!
I said earlier that one way to try to train a model is to take the approach of "start with random weights and see how well it predicts outputs for the training data then adjust weights to improve it and then run through the training data again and then adjust weights to improve it.." iterations until the model either calculates all of the outputs correctly or gets to within an acceptable range. Well, another way to approach it is to decide how many iterations you're willing to do and to just stop the training at that point. Each iteration is referred to as an "epoch" and you might decide that you will run this training process for 500 epochs and then test the model that results against your test data to see how accurate it is. Depending upon your training data, this may have the advantage that the resulting model will not have an acceptably low error rate but one advantage that it definitely does have is that the training process will end - whereas if you were trying to train a model that doesn't have any hidden layer of neurons and the training data is not linearly separable then the training process would never end if you were going to let it run until it was sufficiently accurate because it's just not possible for a model of that form to be accurate for that sort of data.
This gives us a better way to answer the question "how many layers should the model have?" because you could start with just an input layer and an output layer, with randomly generated connection weights (as we always start with), have the iterative run-through-the-input-data-and-check-the-outputs-against-the-expected-values-then-try-to-improve-the-weights-slightly-to-get-better-results process run for 500 epochs and then see how well the resulting model does as handling the test data (for each of the 10k labelled images, run them through the model and count it as a pass if the output that matches the correct digit for the image has the highest value out of all ten of the outputs and count it is a fail if that is not the case).
Since we're not looking at code here to perform all this work, you'll have to take my word for what would happen - this simple model shape would not do very well! Yes, it might predict the correct digit for some of the inputs but even if a broken clock is right twice a day!
This indicates that we need a different model shape and the only other shape that we've seen so far has an additional "hidden layer" between the input layer and the output layer. However, even this introduces some questions - first, if we add a hidden layer then how many neurons should it have in it? The XOR example has two neurons in the input layer, two neurons in the hidden layer and one neuron in the output layer - does this tell us anything about how many we should use here? Secondly, is there any reason why we have to limit ourselves to a single hidden layer? Could there be any advantages to having multiple hidden layers (say, the input layer, a first hidden layer, a second hidden layer, the output layer)? If so, should each hidden layer have the same number of neurons as the other hidden layers or should they be different sizes?
Well, again, on the one hand, we now have a mechanism to try to answer these questions - we could guess that we want a single hidden layer that has 100 neurons (a number that I've completely made up for the sake of an example) and try training that model for 500 epochs* using the training, then see how accurate the resulting model is at predicting the results of the test data. If the accuracy seems acceptable then you could say that you've found a good model! But if you want to see if the accuracy could be improved then you might try repeating the process but with 200 neurons in the hidden layer and trying again - or maybe even reducing it down to 50 neurons in the hidden layer to see how that impacts the results! If you're not happy with any of these results then maybe you could try adding a second hidden layer and then playing around with how many neurons are in the first layer and the second layer!
* (This 500 value is also one that I've just made up for sake of example right now - deciding how many iterations to attempt when training the model may come down to how much training data that you have because the more data that there is to train with, the longer each iteration will take.. so if 500 epochs can be completed in a reasonable amount of time then it could be a good value to use but if it takes an entire day to perform those 500 iterations then maybe a small number would be better!)
One thing to be aware of when adding hidden layers is that the more layers that there are, the more calculations that must be performed as the model is trained. Similarly, the more neurons that there are in the hidden layers, the more calculations there are that must be performed for each training iteration/epoch. If you have a lot of training data then this could be a concern - it's tedious to fiddle around with different shapes of models if you have to wait hours (or even days!) each time that you want to train a model in a new configuration. And so erring on the side of fewer layers and few neurons in those layers is a good starting point - if you can get good results from that then you will get over the finish line sooner!
To finally offer some concrete advice, I'm going to quote a Stack Overflow answer that repeats a rule of thumb that I've read in various other places:
(i) number of hidden layers equals one;
and (ii) the number of neurons in that layer is the mean of the neurons in the input and output layers.
This advice recommends that we start with a single hidden layer and that it have 397 neurons (which is the average of the number of neurons in the input layer = 28 * 28 pixels = 784 inputs and the number of neurons in the output layer = 10).
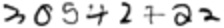
Using the MNIST training data to train a neural network of this shape (784 inputs, 387 neurons in hidden layer, 10 outputs) across 10 epochs will result in a model that has 95.26%* accuracy when the test data is run through it. Considering what some of these handwritten digits in the test data look like, I think that that is pretty good!
* (I know this because I went through the process of writing the code to do this a few years ago - I was contemplating using it as part of a series of posts about picking up F# if you're a C# developer but I ran out of steam.. maybe one day I'll pick it back up!)
To try to put this 95.26% accuracy into perspective, the PDF "Formal Derivation of Mesh Neural Networks with Their Forward-Only Gradient Propagation" claims that the MNIST data has an "average human performance of 98.29%"* (though there are people on Reddit who find this hard to believe and that it is too low) while the state of the art error rate for MNIST (where, presumably, the greatest machine learning minds of our time compete) is 0.21%, which indicates an accuracy of 99.71% (if I've interpreted the leaderboard's information correctly!).
* (Citing P. Simard, Y. LeCun, and J. Denker, "Efficient pattern recognition using a new transformation distance" in Advances in Neural Information Processing Systems (S. Hanson, J. Cowan, and C. Giles, eds.), vol. 5, pp. 50–58, Morgan-Kaufmann, 1993)
Note: If I had trained a model that had TWO hidden layers where, instead of there being a single hidden layer whose neuron count was 1/2 x number-of-inputs-plus-number-of-outputs, the two layers had 2/3 and 1/3 x number-of-inputs-plus-number-of-outputs then the accuracy could be increased to 97.13% - and so the advice above is not something set in stone, it's only a guideline or a starting point. But I don't want to get too bogged down in this right now as the section just below talks more about multiple hidden layers and about other options, such as pre-processing of data; with machine learning, there can be a lot of experimentation required to get a "good enough" result and you should never expect perfection!
Other shapes of network and other forms of processing
The forms of neural network that I've shown above are the most simple (regardless of how many hidden layers there are - or aren't) but there is a whole range of variations that offer tools to potentially improve accuracy and/or reduce the amount of time required to train them. This is a large topic and so I won't go deeply into any individual possibility but here are some common variations..
Firstly, let's go back to thinking about those hidden layers and how many of them that you might want. To quote part of a Quora answer:
There is a well-known problem of facial recognition, where computer learns to detect human faces. Human face is a complex object, it must have eyes, a nose, a mouth, and to be in a round shape, for computer it means that there are a lot of pixels of different colours that are comprised in different shapes. And in order to decide whether there is a human face on a picture, computer has to detect all those objects.
Basically, the first hidden layer detects pixels of light and dark, they are not very useful for face recognition, but they are extremely useful to identify edges and simple shapes on the second hidden layer. The third hidden layer knows how to comprise more complex objects from edges and simple shapes. Finally, at the end, the output layer will be able to recognize a human face with some confidence.
Basically, each layer in the neural network gets you farther from the input which is raw pixels and closer to your goal to recognize a human face.
I've seen various explanations that describe hidden layers as being like feature inputs for increasingly specific concepts (with the manager decision example, the two input neurons represented very specific features that we had chosen for the model whereas the suggestion here is that the neurons in each hidden layer represent features extracted from the layer before it - though these features are extracted as a result of the training process and they may not be simple human-comprehendible features, such as "strategic value").. but I get the impression that this is something of an approximation of what's going on. In the face detection example above, we don't really know for sure that the third hidden layer really consists of "complex objects from edges and simple shapes" - that is just (so far as I understand it) an approximation to give us a feeling of intuition about what is going on during the training process.
It's important to note that ALL that is happening during the training is fiddling of neuron connection weights such that the known inputs of the training data get closer to producing the expected outputs in the training data corresponding to those inputs! While we might be able to understand and describe this as a mathematical process (and despite these neural network structures having been inspired by the human brain), we shouldn't fool ourselves into believing that this process is "thinking" and analysing information in the same way that we do! I'll talk about this a little more in the section "The dark side of machine learning predictions a little further down".
Another variation used is what "activation function" is used for neurons in each layer. When I described the sigmoid function earlier, which took the sums of the neurons in the previous layer multiplied by their connection weights and then applied a formula to squash that value into the 0-1 range; that was an activation function. In the XOR example earlier, the sigmoid function was used as the activation function for each neuron in the hidden layer and each neuron in the output layer. But after I did this, I had to look at the final output values and say "if it's 0.5 or more then consider it to be a 1 and if it's less than 0.5 then consider it to be a 0".. instead of doing that, I could have used a "step function" for the output layer that would be similar to the sigmoid function but which would have sharp cut off points (for either 0 or 1) instead of a nice smooth curve*.
* (The downside to using a step function for the output of a binary classifier is that you lose any information about how confident the result is if you only get 0 or 1; for example, an output of 0.99 indicates a very confident >= 0.5 result while an output of 0.55 is still >= 0.5 and so indicates a 1 result but it is a less confident result - if the information about the confidence is not important, though, then a step function could have made a lot of sense in the XOR example)
Another common activation function that appears in the literature about neural networks is the "Rectified Linear Unit (ReLU)" function - it's way out of the scope of this post to explain why but if you have many hidden layers then you can encounter difficulties if you use the sigmoid function in each layer and the ReLU can ease those woes. If you're feeling brave enough to dig in further right now then I would recommend starting with "A Gentle Introduction to the Rectified Linear Unit (ReLU)".
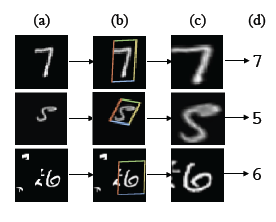
Finally, there are times when changing your model isn't the most efficient way to improve its accuracy. Sometimes, cleaning up the data can have a more profound effect. For example, there is a paper Spatial Transformer Networks (PDF) that I saw mentioned in a StackOverflow answer that will try to improve the quality of input images before using them to train a model or to make a prediction on test data or not-seen-before data.
In the case of the MNIST images, it can be seen to locate the area of the image that looks to contain the numeral and to then rotate it and stretch it such that it will hopefully reduce the variation between the many different ways that people write numbers. The PDF describes the improvements in prediction accuracy and also talks about using the same approach to improve recognition of other images such as street view house numbers and even the classification of bird species from images. (Unfortunately, while the StackOverflow answer links to a Google doc with further information about the performance improvements, it's a private document that you would have to request access to).
The approach to image data processing can also be changed by no longer considering the raw pixels but, instead, deriving some information from them. One example would be to look at every pixel and then see how much lighter or darker it is than its surrounding pixels - this results in a form of edge detection and it can be effective at reducing the effect of light levels in the source image (in the case of a photo) by looking at the changes in brightness, rather than considering the brightness on a pixel-by-pixel basis. This changes the source data to concentrate more on shapes within the images and less on factors such as colours - which, depending upon the task at hand, may be appropriate (in the case of recognising handwritten digits, for example, whether the number was written in red or blue or green or black shouldn't have any impact on the classification process used to predict what number an image contains).

(In my post from a couple of years ago, "Face or no face", I was using a different technique than a neural network to train a model to differentiate between images that were faces and ones that weren't but I used a similar method of calculating "intensity gradients" from the source data and using that to determine "histograms of gradients (HoGs)" - I won't repeat the details here but that approach resulted in a more accurate model AND the HoGs data for each image was smaller than the raw pixel data and so the training process was quicker; double win!)
The next thing to introduce is a "convolutional neural network (CNN)", which is a variation on the neural network model that adds in "convolution layers" that can perform transformations on the data (a little like the change from raw colour image data to changes-in-brightness data, as shown in the edge detection picture above) though they will actually be capable of all sorts of types of alteration, all with multiple configuration options to tweak how they may be applied. But..
a CNN learns the values of these filters on its own during the training process
(From the article "An Intuitive Explanation of Convolutional Neural Networks")
.. and so the training process for this sort of model will not just experiment with changing the weights between neurons to try to improve accuracy, it will also try running the entire process over and over again with variations on the convolutional layers to see if altering their settings can produce better results.
To throw another complication into the mix - as I mentioned earlier, the more hidden layers (and the more neurons that each layer has), the more calculations that are required by the training process and so the slower that training a model will be. This is because every input neuron is connected to every neuron in the first hidden layer, then every neuron in the first hidden layer is connected to every neuron in the second hidden layer, etc.. until every neuron in the last hidden layer is connected to every neuron in the output layer - which is why the number of calculations expands massively with each additional layer. These are described as "fully-connected layers". But there is an alternative; the imaginatively-named approach "sparsely connected layers". By having fewer connections, the necessary calculations are fewer and the training time should be shorter. In a neural net, there are commonly a proportion of connections that have a great impact on the accuracy of the training model and a proportion that have a much lower (possibly even zero) effect. Removing these "lower value" connections is what allows us to avoid a lot of calculations/processing time but identifying these connections is a complex subject. I'm not even going to attempt to go into any detail in this post about how this may be achieved but if you want to know more about the process of intelligently selecting what connections to use, I'll happily direct you to the article "The Sparse Future of Deep Learning!
One final final note for this section, though: in most cases, more data will get you superior results in comparison to trying to eke out better results from a "cleverer" model that is trained with less data. If you have a model that seems decent and you want to improve the accuracy, if you have the choice between spending time obtaining more quality data (where "quality" is an important word because "more data" isn't actually useful if that data is rubbish!) or spending time fiddling with the model to try to get a few more percentage points of accuracy, generally you will be better to get more data. As Peter Norvig, Google's Director of Research, was quoted as saying (in the article "Every Buzzword Was Born of Data"):
We don't have better algorithms. We just have more data.
The dark side of machine learning predictions
The genius of machine learning is that it can take historical data (what inputs lead to what output) and produce a model that can use that information to make an output prediction for a set of inputs that it's never seen before.
A big downfall of machine learning is that all it is doing is taking historical data and producing a model that uses that information to predict an output for a set of inputs that it's never seen before.
In an ideal world, this wouldn't be a downfall because all decisions would have been made fairly and without bias. However.. that is very rarely the case and when a model is trained using historical data, you aren't directly imbuing it with any moral values but it will, in effect, exhibit any biases in the data that was used to train it.
One of the earliest examples that stick in my mind of this was of a handheld camera that had blink detection to try to help you get a shot where everyone has their eyes open. However, the data used to train the model used photos of caucasian people, resulting in an Asian American writing a post "Racist Camera! No, I did not blink... I'm just Asian!" (as reported on PetaPixel) as the camera "detected" that she was blinking when she wasn't.
And more horrifying is the article from the same site "Google Apologizes After Photos App Autotags Black People as 'Gorillas'" which arose from Flickr adding an auto-tagging facility that would make suggestions as to what it recognised in your photos. Again, this comes down to the source data that was used to train the models - and it's not to suggest that the people sourcing and using this data (which could well be two groups of people; one that collects and tags sets of images and a second group that presumes that that labelled data is sufficiently extensive and representative) are unaware of the biases that it contains. As with life, there are always unconscious biases and the only way to tackle them is to be aware of them and try as best you can to eradicate them!
Another example is that, a few years ago, Amazon toyed with introducing a resume-screening process using machine learning - where features were extracted from CVs (the features would be occurrences of a long, known list of words or phrases in this case, as opposed to the numeric values in the manager decision example of the pixel brightnesses in the MNIST example) and the recruitment outcomes (hired / not-hired) from historical data to train a model. However, all did not go to plan. Thankfully, they didn't just jump into the deep end and accept the results of the model when they received new CVs; instead, they ran them through the model and performed the manual checks, to try to get an idea of whether the model was effective or not. I'm going to take some highlights from the article "Amazon built an AI tool to hire people but had to shut it down because it was discriminating against women", so feel free to read that if you want more information. The upshot is that historically there had been many more CVs submitted by men than women, which resulted in there being many more "features" present on male CVs that resulted in a "hire them!" result. As I described before, when a neural network (presuming that Amazon was using such an approach) is presented with many features, it will naturally work out which have a greater impact on the final outcome and the connection weights for these input neurons will be higher. What I didn't describe at that point is that the opposite also happens - features that are found to have a negative impact on the final outcome will not just be given a smaller weight, they will be given a negative weight. And since this model was effectively learning that men are more likely to be hired and women are less likely, the model that it ended up with gave greater positive weight to features that indicated that the CV was for a male and negative weight to features that indicated that the CV was for a female, such as a mention of them being a "women's chess club captain" or even if they had attended one of two all-women's colleges (the name of which had presumably been in the list of known words and phrases that would have been used as features - and which would not have appeared on any man's CV). The developers at Amazon working on this project made changes to try to avoid this issue but they couldn't be confident that other biases were not having an effect and so the project was axed.
There are, alas, almost certainly always going to be issues with bias when models are trained in this manner - hopefully, it can be reduced as training data sets become more representative of the population (for cases of photographs of people, for example) but it is something that we must always be aware of. I thought that some industries were explicitly banned from applying judgements to their customers using a non-accountable system such as the neural networks that we've been talking about but I'm struggling to find definitive information. I had it in my head that the UK car insurance market was not allowed to produce prices from a system that isn't transparent and accountable (eg. it would not be acceptable to say "we will offer you this price because the computer says so" as opposed to a "decision-tree-based process" where it's essentially like a big flow chart that could be explained in clear English, where the impacts on price for each decision are based on statistics from previous claims) but I'm also unable to find any articles stating that. In fact, sadly, I find articles such as "Insurers 'risk breaking racism laws'" which describe how requesting quotes from some companies, where the only detail that varies between them is the name (a traditionally-sounding white English name compared to another traditional English - but not traditionally white - name, such as Muhammad Khan), results in wildly different prices being offered.
Talking of training neural nets with textual data..
In all of my descriptions before the previous section, I've been using examples where the inputs to the model as simple numbers -
- Zeros and ones for the AND, OR, XOR cases
- Numeric 0..1 value ranges for the features of the manager decision example (which were, if we're being honest, oversimplifications - can you really reliably and repeatedly rate the strategic importance to the company of a single feature in isolation? But I digress..)
- Pixel brightness values for the MNIST example, which are in the range 0-255 and so can easily be reduced down to the 0-1 range
- I mentioned brightness gradients (rather than looking at the intensity of individual pixels, looking at how much brighter or darker they are compared to surrounding pixels) and this also results in values that are easy to squeeze into the 0-1 range
However, there are all sorts of data that don't immediately look like they could be represented as numeric values in the 0-1 range. For example, above I was talking about analysis of CVs and that is purely textual content (ok, there might be the odd image and there might be text content in tables or other layouts but you can imagine how simple text content could be derived from that). There are many ways that this could be done but one easy way to imagine it would be to:
- Take a bunch of documents that you want to train a classifier on (to try to avoid the contentiousness of the CV example, let's imagine that it's a load of emails and you want to automatically classify them as "spam", "company newsletter", "family updates" or one of a few other categories
- Identify every single unique word across all of the documents and record them in one big "master list"
- Go through each document individually and..
- Split it into individual words again
- Go through each word in the master list and calculate a score by counting how many times it appears in the current document divided by how many words there are in the document (the smaller that this number is, the less common that it is and, potentially, the more interesting it is in differentiating one document from another)
- For each document, you now have a long list of numbers in the range 0-1 and you could potentially use this list to represent the features of the document
- Each list of numbers is the same length for each document because the same master list of words was used (this is vitally important, as we will see shortly)
- The list of numbers that is now used to describe a given document is called a "vector"
One problem here is that the vocabulary used throughout these emails could be very large, meaning that the master list would be very large and the list of numbers for each document equally large. The input layer of a neural network that we would train using this data would have to have as many neurons as there are entries in these lists. This might not necessarily be a problem because it is possible to train large neural networks - but the larger that they are, the longer that it takes.
There are almost certainly going to be lots of words that appear that will have no effect on the classification of an email - words like "a" and "the", for example. As discussed earlier, this is also not strictly a problem because features that have little effect on the classification of data will naturally end up with low connection weights in the final trained model. However, it feels wasteful to throw data into the mix that we know isn't going to be useful but is certainly going to slow down the training process by forcing it to perform many more calculations. One approach is to ignore "stop words" when generating the master list of all words in the source data -
Stopwords are the words in any language which does not add much meaning to a sentence. They can safely be ignored without sacrificing the meaning of the sentence.
(From "Stop Words in NLP")
This is a common approach and lists of stop words are freely available - but it's important to be aware that they are language-dependent; English stop words are not the same as French stop words, for example, and you will need to consider this if you're not always working with English language data!
Another approach is to take advantage of the fact that the calculation above generates smaller values for words that are potentially more relevant (because the word "the" is likely to appear many times in a document, if you divide the number of times that it appears by the total number of words in the document then that value will normally be much higher than if you divided the number of time that a less common word - like "bonus" - appeared in a document by the total number of words in that document). You might decide to discard, say, 20% of the words by looking at which of them appear in the documents with a high score and removing those words from the master list (and removing the corresponding entries from each of the lists of numbers that represents each document). By doing so, you would likely end up removing the stop words without having to have had to start with a known list of stop words to get rid of! (Again, this sort of process is language-dependent because words that are common in one language are different in another language and this sort of approach will work best if all of the documents used as training data are written in the same language).
This still leaves us with many more distinct words than is probably optimal. For example, if the document text is split into words in a very simple manner (such as breaking on whitespace) then you may have an email that is a thrilling update about Mark's cat, while another email may be talking about Henry's cats - in the context of trying to working out what an email is talking about, is there any meaningful distinction between "cat" (singular) and "cats" (plural)? Probably not. And so adding in a pre-processing step to the act of splitting the text into individual words could help reduce the number of distinct words further by grouping words that are probably equivalent. An example of this is the Snowball Stemmer which performs simple transformations such as lower-casing content, removing punctuation and removing common endings from words so that different forms of verbs are combined into the same word; eg.
Dan's cats like going to the park
.. becomes
dan cat like go to the park
(There is unlikely to be any benefit to considering the words "Dan's" and "Dan" as different features, just as there is little benefit to considering "cat" and "cats" as unique features).
Note that the Snowball Stemmer is also language-dependent and so you need to know what language the text that you're working with is in - again, if you're lucky enough to be dealing with an entirely English set of training documents then that's fine.. though the nltk.stem.snowball Python package used in the link above has support for different languages, so long as you tell it which language you want it to use.
(Shameless plug: Some years ago, I wrote my own interpretation of a Full Text Indexer - which actually powers the site search on this blog! - and core functionality for that include "tokenising" and "token normalising", which are the splitting of a string of text into individual words and the transformation of those tokens such that equivalent tokens like "Cat" and "cat" and "cats" are all reduced down to a single string; if you wanted to see one way to do this sort of work in C# then you could poke around my FullTextIndexer GitHub repo or read some of the articles listed in my "Full Text Indexer Post Round-up".. I would be remiss if I didn't mention that there are plenty of other libraries for .NET that have been written in the last ten years that are quite likely more featureful and optimised, but this is my blog and so if I want to link to my own code instead then I will! :))
In general, it would make sense to apply the stemming logic before culling the most common words from the list of features, so that you have an accurate picture of what words are true most "interesting" (ie. uncommon).
When I described the way that you might approach an MNIST classifier earlier, I explained that you could get a surprisingly accurate model by flattening out the 28x28 pixel image into one long 784 list of values - seemingly discarding structural information about where the pixels appear in relation to each other in two dimensions. What I've described just now, regarding the words-as-features, is similar in some ways as it is also discarding information about how words appear in relation to each other; the features that are produced are all solely based on individual words in isolation.
However, with natural language, the words that appear around a given word can make a big difference - the word "new" represents an entirely different concept when it talks about releasing a "new feature" for some software to when it is used in the city name "New York". As such, depending upon the data and the task in hand, it will often result in a more accurate model if the features extracted from textual content are not only individual words but also phrases, such as adjacent pairs of words (like "New York") or concurrent runs of three words or even more. Doing so will mean that the number of possible features grows again (it's not just a master list of individual words any longer, it's now a list of words and phrases - and one of the decisions that you will have to make is how long you allow the extracted phrases to be. The longer that they can be, the more possible features that you will produce (which will make model-training slower). The shorter that they can be, the fewer features there will be (and so model-training will be faster) but you risk missing out on vital context if the limit is too low (and so you might end up training models relatively quickly but finding that their accuracy is low for the task at hand).
With this knowledge, you could now picture a neural network model because you can take the documents in your training data and convert them into vectors (which are, as a reminder, simply lists of numeric values) and each vector will be the same length (ie. it will have the same number of values in it). The length of this vector will determine how large the input layer is in the neural network because there must be as many neurons in the input layer as the document vectors are long (if, say, the master list of words used to generate the document vectors had 10,000 unique entries then each document will have been translated into a vector with 10,000 values in it and the input layer for the neural network will have to have 10,000 nodes).
This brings us to an important decision.. we will have to decide how large the document vectors should be - before, I said that you might discard the least interesting 20% of the words but that was just an example figure that I made up on the spot. I started this example by saying that you may wish to classify emails into a particular set of categories but you will have had to decide on what exactly is in that "what type of email is this" list before you can create a model and you'll need to have manually classified every document in your training data before you can start training a neural net to do the same work. The idea behind training a classifier is that it can predict a category for data (eg. an email) that it's never seen before but it needs historical labelled data to do that, which is what this pre-categorised training data will be.
All of the variables that have been mentioned - the percentage of "non-interesting" words (or "tokens", as they are often referred to) that are discarded, the maximum number of tokens that may be combined into one to produce larger features (like the "New York" example), the number of outputs (which is the number of categories that emails may be assigned to - which will dictate how many neurons in the output layer; one per category), how many hidden layers that your model should have (and how large those layers should be).. these will all impact the training process and are known as "hyperparameters". Changing some of them may result in large changes (good or bad) in the accuracy of the trained model while changing others may not have much impact at all. As I said before, part of working with machine learning is in experimenting with different models and different hyperparameters to see what works well for your data and what doesn't!
Side note: The process that I've described above (about producing a "master list" of words and phrases) is a sort of simplified/bastardised of TF-IDF ("term frequency-inverse document frequency" - ie. how often do individual words appear in a document relative to the total number of words in that document), for which there is a nice intro at "Understanding TF-ID: A Simple Introduction". And when I spoke about the process of combining multiple individual words together to produce new tokens (such as "New York"), those new tokens are referred to as "n-grams" - so if you want to find out more about all this then there is plenty of great information out there!
Other types of machine learning
Almost the entirety of this lengthy post has been about neural network classifiers but it's definitely worth mentioning that these are not the only type of machine learning techniques.
The first example that I want to talk about is "document similarity" - say you have 100,000 text documents and you are fairly sure that some of them are very nearly duplicates of each other (maybe one is a technical spec for an audio amplifier from 2019 and another is a revision of that document from 2020 that includes some corrections but is basically the same), how would you find these similar documents? Well, a good starting point would be by using the textual content feature extraction described in the previous section - ie. converting each document into a vector. When that is done, it's actually quite simple to come up with an approximate "distance measurement". If you imagine a load of 2D points on a graph, you can easily measure the distance between any two points by using Pythagorean theorem; take the horizontal difference between the two points and square it, add that to the vertical difference between them squared, then square root the result. This same approach works for points in a 3D world. And the same principle works for points with any number of dimensions - and this is how we could imagine our vectors that have been generated from each document, as points in some crazy world with many, many dimensions. We can measure the distances between pairs of these points and pairs that are relatively close to each other are likely to correspond to documents that are fairly similar in content, while pairs of points that are further away will correspond to documents that are less similar to each other.
Now, this doesn't actually involve any machine learning - it's just extracting features from documents and then measuring the distances between every single pair of points. If you only have 100 documents then these calculations can probably be performed so quickly that it wouldn't pose any sort of problem but if we go back to imagining 100,000 documents (or even imagining millions of documents, if not more!) then calculating the distances between every single pair of documents in that list could become a gargantuan task (as in, performing the calculations in a "brute force" approach - where every single distance is individually calculated - could potentially take a computer longer to compute than you have left to live, which would be very sad). There are clever machine learning algorithms that work out how to approximate these calculations such that the brute force approach is not necessary while still ensuring that document similarity measures for all of your data remain attainable (one such algorithm is "Hierarchical Navigable Small World (HNSW)", which is way too technical for me to do anything about but mention here in passing). Something interesting to note about this technique is that it is an example of "unsupervised" learning - when we looked at the MNIST (handwritten digit recognition) example earlier, that required that the input data was all labelled so that the machine could learn how the images compared or differed to each other - in this case, though, there is no such labelling required; we just tell the computer to go off and work out on its own what documents look like other documents!
(Last year, I wrote a post about how I was using a C# machine learning library that a company that I used to work for published to automatically generate "You may also be interested in" links for each of my blog posts and that used some of the same techniques described here; the FastText algorithm automates the extraction of features from textual data and HNSW calculates distances between the document vectors - I don't actually have anywhere near enough posts on my blog for this to be necessary, I just wanted to try it for fun! If you want to find out more, see "Automating suggested / related posts links for my blog")
The next example is another form of binary classifier. I mentioned earlier my post "Face or no face", where I wanted to write code that could look at a photo and identify areas in it that appeared to be people's faces. There was a bunch of pre-processing to take a colour picture, then a very rough algorithm was run to find areas that might potentially be faces - this would return many false positives (ie. sections of a photo that were not faces) and I trained a Support Vector Machine (SVM) to be able to predict with much greater accuracy whether these image subsections were indeed faces or not. An SVM is trained by giving it a large list of labelled points (where a point doesn't have to be 2D or 3D, it can have many dimensions - so its' vectors again, in other words) and leaving it to try to work out a way to split those points so that all of the points on one side of the line are of one category and all of the points on the other side are of another category. We could train an SVM with the data from the manager decision example from earlier - its training data would be the historical list of 2D points (where the dimensions represented "strategic value to the company" and "percentage that customer will pay for feature development cost") and whether the manager gave a yes or no answer and the SVM would try to find a line that splits (or "delineates") those historical points. In a somewhat comparable way to the training of a neural network, it will pick a line at random, see how well or poorly that line delineates the results, adjusts the line to try to improve the situation and then repeats and repeats until it manages to split the data effectively. The vectors for the face-or-no-face code were much larger than two dimensions and so it's no longer a case of finding a 1D line that splits points on a 2D plane; instead, it is (cue impressive-sounding technical terms!) a case of finding an {n-1} dimensional "hyperplane" that splits the {n} dimensional space that the vector points exist in. The training data for the face-or-no-face SVM was derived from the publicly accessible "Caltech 10, 000 Web Faces".
I first mentioned unsupervised classification right near the start of this post, where training data will consist of points that should be arranged into groups of other points that they are most similar to. The problem is that the computer has no way of coming up with a description for what this group represents and so it is less directly useful for classifying into categories as those categories don't come with titles! However, it could be feasibly be used by someone like Netflix when they want to come up with creative new categories - they could have the computer extract features from tv shows and films (where the features may actually be extracted from metadata about the programs, such as description or even public reviews) and then have it arrange them into groups, which a Netflix employee could manually poke around in to see if a theme presents itself that could be used as a new niche category. But this still feels quite nebulous and so maybe a concrete example may help. One of the hyperparameters that you will need to set is how many groups you want to be generated, so let's go back to the MNIST data and imagine that we want to give a machine-learning algorithm all of the source images and for it to split the data into ten groups (for the digits 0..9) but without giving it any labels for that source data (in contrast to the supervised learning approach that was described before). Well, one such algorithm is "t-distributed stochastic neighbour embedding (t-SNE)" and that can produce results such as the following:
(Reproduced under license terms on Kyle McDonald's Flickr album page)
The t-SNE takes vectors with 784 dimensions (since the MNIST data is a set of 28x28 pixel images) as input and returns a vector for each of them that has only two dimensions, which is how the results can be plotted on the graph above. This is known as "dimension reduction" (since the 2D vectors are essentially approximations of the original 784-dimension vectors). One that image, the labels for each of the MNIST images (ie. whether that image is the digit 0 or 1 or .. 9) are used to determine the colour to draw the point as - but this is only to illustrate the results of the t-SNE algorithm, those labels were not used as part of the training. And so it's quite amazing just how effective it is at grouping similar digits together! (If there were big groups that were full of intermingled colours then that would indicate a poor job but the fact that the groups are so distinct, with only a few outliers here and there, suggests that it's done a fantastic job!) Of course, one part of the reason that it does such a good job of separating the images for each digit is that the hyperparameter specified for the algorithm about the number of groups that it should try to identify is set to 10 - if it had been set to 3 or to 12 (or to anything else) then the groupings wouldn't have been so obviously correct.
Another unsupervised algorithm that is similar to t-SNE is "Uniform Manifold Approximation and Projection (UMAP)", which you can find available as a C# implementation (also published by the company that I worked for that released the machine learning library; Curiosity!) in case you are a .NET developer and want to try it out. The "Tester" project in there includes a binary file containing the MNIST image data and it will use this to train a model that groups together the images that it thinks are similar and then generates a bitmap of the results that looks similar to the image shown above. Nothing is forcing this algorithm to reduce the vectors to two dimensions, in case you were wondering - that also is a hyperparameter that is set to train the model. It could be set to 3 and it would generate 3-dimensional vectors that could be plotted in 3D space, rather than the 2D graph above.
So machine learning is always the most amazing-est thing, right (except when it's evil and discriminatory)?
I know that I've just written thousands of words espousing the power of machine learning but I did also start the post by giving an example of coding in a "classic approach" - summing up a list of purchases that someone has made, ensuring that the correct tax is included for each of them. This is a simple and predictable process and there would not be any benefit to trying to replace this with a machine learning system. For adding together costs and calculating tax, absolute precision is expected and known predictable rules are in place; machine-trained models will almost always have some level of error (much as we may try to tweak the model to minimise it) and they are very often difficult (if not impossible) to definitively reason about - so if someone disputed a bill that had been generated from a machine-trained model, it would be very difficult to justify why it was correct or not!
However, there are some middle grounds where you may be tempted to go one way or the other. The first example that comes to mind is that where I used to work, the CTO took the opportunity to learn how to write a Roslyn analyser by implementing a "Stop commenting out code (delete it if you don't need it - we have source control, you know!)" analyser. Roslyn (well, the ".NET Compiler Platform SDK (Roslyn APIs) if you're being pernickety) makes it easy to locate comments and to show warnings in the Error List relating to them if you want to, but how to decide whether the comment text is C# code or whether it's a useful explanatory message? He could have:
- Performed a one-off analysis of the code base and extracted all of the comments
- Taken a random subset of those comments (say 5% - it was a large codebase, so even that might have been too high!)
- Manually classified each of the comments as "code" or "not code"
- Decided on a text-based feature extraction process to translate each piece of text into a vector, resulting in a list of labelled (as either 0 for "not code" or 1 for "code") vectors
- Trained a binary classifier using those labelled vectors (perhaps splitting it up to use 70% of them as training data and 30% as test data)
- Potentially spent time fiddling with the hyperparameters used in the training until the accuracy of the model was sufficiently high, based upon the results of running the test data through it
- Exported that classifier model as C# code that the analyser could execute so that it could record warnings against comments that looked they were commented-out code
Alternatively, he could have come up with a system that tried to guess whether a comment was commented-out code or something useful by splitting it into tokens (ie. individual words and symbols), assigning a score (either positive or negative) to a set of known tokens and then adding up the total for the tokens in the comment. For example, a curly brace symbol may have a positive score since they are much more common in C# code than in English phrases. If the score is greater than a particular threshold then the analyser will decide that it's probably commented-out code and record a warning about it.
This may not be quite as easy as you might expect because you can't just assign a positive score to every keyword in the C# language otherwise comments like this:
// this should be a private class
.. might be identified as commented-out code because it contains the keywords "private" and "class", but that would be wrong! And so there would be a fine line to walk to try to get it right for at least enough of the time.
(In case you were wondering, he went with the second option and it ended up working pretty well!)
A final example is a project that I only heard about very recently and just thought that it was ingenious! PawSense will "catproof your computer" because:
When cats walk or climb on your keyboard, they can enter random commands and data, damage your files, and even crash your computer. This can happen whether you are near the computer or have suddenly been called away from it.
PawSense is a software utility that helps protect your computer from cats. It quickly detects and blocks cat typing, and also helps train your cat to stay off the computer keyboard.
This might sound like the sort of thing that you would somehow try to train a model for because surely the difference between me hammering the keys and a cat jumping on the keyboard and smashing some down could be quite subtle?? Having said that, I don't personally have any great intuition for this because the closest that my cats get to this is when they lie down too close to the keyboard and end up leaning down some weight on one of the keys near the edge - they don't actually walk across it. However, the author of this software used some simple observations that are explained in the FAQ on the site, that:
If you carefully measure cat paws, you will find that practically all cat paws are significantly larger than a typical keyboard key. When a cat first places its paw down, the cat's weight plus the momentum of the cat's movement exerts pounds of force on the keyboard, primarily through the cat's paw pads.
The cat's paw angles and toe positions also undergo complex changes while the paw lands on the keyboard. This forces keys and often key combinations down in a distinctive style of typing which includes unusual timing patterns.
Cats' patterns of overall movement in walking or lying down also help make their typing more recognizable.
So simple! And yet, when you read the briefer description from the home page:
PawSense constantly monitors keyboard activity. PawSense analyzes keypress timings and combinations to distinguish cat typing from human typing.
.. then you could be forgiven for imagining that something much more convoluted would be required and that somehow the author of this software acquired lots of sample data of him (and other humans) typing in various manners (because keyboard interaction varies hugely depending upon whether you're scrolling through a web site or if you're typing code or if you're writing prose) and compared it to lots of samples of cats interacting with a keyboard. But, thinking about it, trying to record lots of keyboard interactions by cats sounds extremely difficult to me - they like to do what they want to do and are not likely to be coerced into keyboard walking if they don't already feel in the mood to do so!
You can see, then, that it's not only programs that have an extremely simple-looking set of interactions (such as the summing of item costs and taxes) that are better done by writing a traditional algorithm, there are also lots of programs that look like they exhibit "fuzzy" or "intelligent" behaviour where there is no clever machine learning involved, it is simply a result of clever observations and experimentation by whoever designed and wrote the code. However, in cases where machine learning can shine it can be incredibly powerful - whether that is YouTube keeping you on the site longer by recommending videos to watch, whether it's an automated categorisation of incoming help desk tickets in a large company to try to get customer problems directed to the relevant departments more quickly, whether it's keeping spam emails out of your inbox or whether it's used to program a cat flap to not let a cat in if it's bringing a "gift" with it (ie. a dead bird or rodent), it makes possible things that traditional algorithms would make very difficult to do well if they could even be done at all. And while it's certainly not in all software, you might be astonished to know just how much directly contains some or interacts with services that do!
Posted at 23:44
Last time:
Parallelising (LINQ) work in C#About
Dan is a big geek who likes making stuff with computers! He can be quite outspoken so clearly needs a blog :)
In the last few minutes he seems to have taken to referring to himself in the third person. He's quite enjoying it.
Recent Posts
- Hosting a DigitalOcean App Platform app on a custom subdomain (with CORS)
- (Approximately) correcting perspective with C# (fixing a blurry presentation video - part two)
- Finding the brightest area in an image with C# (fixing a blurry presentation video - part one)
- So.. what is machine learning? (#NoCodeIntro)
- Parallelising (LINQ) work in C#
Highlights
- Face or no face (finding faces in photos using C# and Accord.NET)
- When a disk cache performs better than an in-memory cache (befriending the .NET GC)
- Performance tuning a Bridge.NET / React app
- Creating a C# ("Roslyn") Analyser - For beginners by a beginner
- Translating VBScript into C#
- Entity Framework projections to Immutable Types (IEnumerable vs IQueryable)
Archives
- April 2025 (1)
- March 2022 (2)
- February 2022 (1)
- August 2021 (1)
- April 2021 (2)
- March 2021 (1)
- August 2020 (3)
- July 2019 (2)
- September 2018 (1)
- April 2018 (1)
- March 2018 (1)
- July 2017 (1)
- June 2017 (1)
- February 2017 (1)
- November 2016 (1)
- September 2016 (2)
- August 2016 (1)
- July 2016 (1)
- June 2016 (1)
- May 2016 (3)
- March 2016 (3)
- February 2016 (2)
- December 2015 (1)
- November 2015 (2)
- August 2015 (3)
- July 2015 (1)
- June 2015 (1)
- May 2015 (2)
- April 2015 (1)
- March 2015 (1)
- January 2015 (2)
- December 2014 (1)
- November 2014 (1)
- October 2014 (2)
- September 2014 (2)
- August 2014 (1)
- July 2014 (1)
- June 2014 (1)
- May 2014 (2)
- February 2014 (1)
- January 2014 (1)
- December 2013 (1)
- November 2013 (1)
- October 2013 (1)
- August 2013 (3)
- July 2013 (3)
- June 2013 (1)
- May 2013 (2)
- April 2013 (1)
- March 2013 (8)
- February 2013 (2)
- January 2013 (2)
- December 2012 (3)
- November 2012 (4)
- September 2012 (1)
- August 2012 (1)
- July 2012 (3)
- June 2012 (3)
- May 2012 (2)
- February 2012 (3)
- January 2012 (4)
- December 2011 (7)
- August 2011 (2)
- July 2011 (1)
- May 2011 (1)
- April 2011 (2)
- March 2011 (3)